La geometría de los copos de nieve. Aproximaciones matemáticas

Ignacio del Amo

Resumen

En esta monografía abordo el tema de la geometría de los copos de nieve. Lo primero que he hecho ha sido buscar por qué los copos de nieve son hexagonales, y es debido a que las moléculas de agua en la naturaleza forman un ángulo muy cercano al que forma el centro un tetraedro regular con sus vértices, y estos tetraedros naturales se unen formando redes moleculares hexagonales, por lo que la forma de los copos de nieve se debe a la geometría estructural del hielo que se forma en la atmósfera.

A continuación, calculo varias características del hexágono en función del lado, no obstante, el hexágono regular proporciona una morfología general de los copos, aunque no tiene en cuenta las ramificaciones, así que basándome en la propiedad del hexágono de descomponerse en seis triángulos equiláteros, calculo las áreas de diferentes tipos de copo tratándolos como polígonos. Y llego a dos conclusiones principales:

• Los copos de nieve se puede descomponer en triángulos equiláteros de distinto o igual tamaño para calcular su área.
• Ningún copo puede tener un área mayor de

Donde A es el área y l el lado del hexágono de menor tamaño que puede contener al copo.

1. Introducción

Cuando pensamos en un copo de nieve, es común pensar en una estrella hexagonal con intrincadas ramificaciones. Aunque los copos pueden tener gran variedad de formas, ésta es la más interesante de todas ellas, por lo que es aquella en la que me voy a centrar para esta monografía. Éste es uno de los grandes ejemplos de la belleza que alcanza la naturaleza y también de la belleza de los objetos matemáticos. Sin embargo, la geometría estudiada desde las matemáticas describe objetos con unas características exactas, que en la naturaleza se dan sólo de forma aproximada. En esta monografía pretendo abordar el tema de la geometría que se da en los copos de nieve hablando sobre por qué se forman así, qué objetos matemáticos se le aproximan más y sus características y calcular el área de los distintos tipos de copos.

Este tema posee interés, además de por las fascinantes formas de los copos, por estar relacionado con una rama de las matemáticas relativamente nueva: la geometría fractal. La geometría fractal ha resultado encontrarse en muchos aspectos de la naturaleza, como la forma de las montañas y las nubes y sus relaciones con crecimiento (y por tanto el código genético) de plantas como las coles o los árboles. El estudio de los fractales ha sido aplicado en campos como la aerodinámica, la metalurgia y la astronomía. Aunque a primera vista parece un tema trivial, el uso de fractales en la cristalografía aplicada a los copos de nieve se está usando para averiguar propiedades de superficie del hielo, esenciales para explicar muchos procesos meteorológicos.

2. Desarrollo

2.1. La geometría hexagonal del hielo

2.1.1. Historia de los copos de nieve

La geometría de los copos de nieve ha sido estudiada por muchas personas a lo largo de la historia. Una de los más relevantes fue Kepler, que escribió un pequeño tratado acerca de ello en 1611 llamado Strena seu de nive sexangula, o El copo de nieve de seis ángulos. En este tratado, Kepler describe su admiración por la forma hexagonal de los copos de nieve y trata de explicarla. Para ello la compara con la simetría pentagonal que se encuentra en la naturaleza, como por ejemplo en las flores. Él explica la geometría pentagonal de las flores diciendo que se debe al número áureo, que está presente en el dodecaedro y en el icosaedro, y está también en el “alma” de las flores. Pero, llegado a este punto, no puede avanzar dado que los copos de nieve no tienen “alma”, así que llega a la conclusión de que hay un principio superior que conecta el calor y el frío, y que explica que haya una forma geométrica de la materia inerte que, como se puede ver en los copos de nieve, es el hexágono¹. También fue importante, aunque en menor medida, el filósofo y matemático René Descartes, que en 1653 hizo una descripción bastante correcta de la morfología de los copos de nieve.

El matemático Helge Von Koch describió en 1904 una interesante curva fractal, que veremos más adelante, llamada curva de Von Koch, con la que se puede formar una figura llamada Copo de Nieve de Von Koch. Otra persona que mencionaré a lo largo de la monografía es Kenneth Libbrecht, profesor de física de la universidad de Caltech, que ha escrito varios artículos científicos que citaré más adelante sobre los copos de nieve. La principal ventaja que tiene este último autor es ser contemporáneo y cuenta con la tecnología del siglo XXI.

2.1.2. La geometría del hielo

Ya hemos visto cuál era la justificación que daba Kepler a la forma hexagonal de los copos de nieve, ahora vamos a ver cuál es la que ha dado la ciencia moderna.

El agua se encuentra normalmente en estado líquido. Cuando está en este estado las moléculas están libres de fuerzas que las cohesionen. Pero cuando pasa al estado sólido las moléculas se organizan mediante puentes de hidrógeno para formar una red cristalina con una geometría particular. Existen quince tipos distintos de hielo dependiendo de las condiciones en las que se forme. Tienen distintas geometrías: pueden ser cúbicos, hexagonales, tetraédricos, romboédricos o monoclínicos². En el siguiente diagrama de fases vienen representados en función de las condiciones de presión y temperatura:

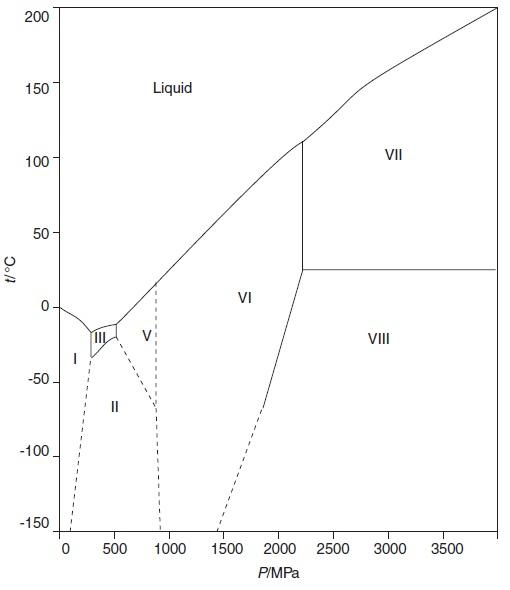
Los copos de nieve se forman en la atmósfera, luego las condiciones de presión son menores a una atmósfera (1atm≈101MPa) y las de temperatura son poco inferiores a 0ºC. Por tanto, el hielo que nos interesa es el hielo tipo I.

En este tipo de hielo las moléculas tienden puentes de hidrógeno en una disposición espacial tetraédrica; los dos átomos de hidrógeno de una molécula A tienden puentes hacia átomos de oxígeno de otras moléculas y, a su vez, el átomo de oxígeno de la molécula A recibe dos puentes. Siguiendo este esquema, cada molécula se transforma en un tetraedro regular con otra molécula en cada uno de sus vértices, formado redes hexagonales⁴. Como veremos en el próximo apartado, los hexágonos pueden ser construidos con seis triángulos equiláteros.

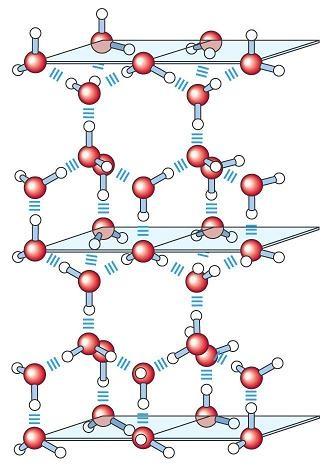
La forma tetraédrica de los enlaces moleculares se distorsiona con la presión, así que, como el hielo I se forma a bajas presiones, su forma se aproximará mucho a la tetraédrica. Para comprobar cuánto se acerca a ella y sabiendo que el ángulo que forman los tres átomos de una molécula de agua es aproximadamente de 105 grados⁶, voy a calcular el centro de un tetraedro regular para ver si el ángulo que éste forma con sus vértices es cercano a 105 grados.

Basándome en el desarrollo del tetraedro regular (un triángulo equilátero con tres triángulos iguales en cada uno de sus lados), he calculado la posición del vértice opuesto al triángulo central calculando las intersecciones de tres esferas de radio l cuyos centros estaban situados en los vértices de dicho triángulo:

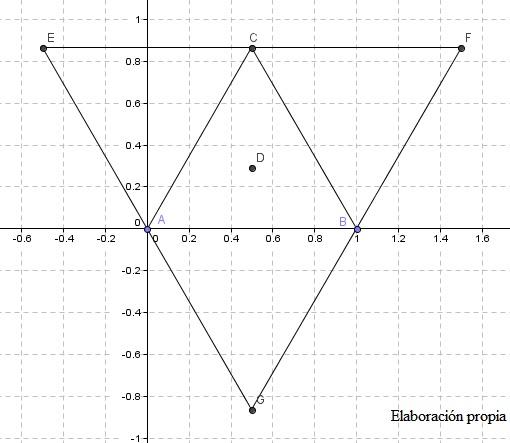
Siendo l el lado de un tetraedro regular con tres vértices coplanarios en A=(0,0,0),

B=(l,0,0) y $C=\left(\frac{l}{2}\mathrm{,0},l\text{sin}(\text{60})\right)$, el cuarto vértice D estará en la intersección positiva de las tres esferas:

$\{\begin{array}{c}{x}^2+y^2+z^2=l^2\\ {\left(x-l\right)}^2+y^2+z^2=l^2\text{sin}(\text{60}{)}^2\\ {\left(x-\frac{l}{2}\right)}^2+y^2+{\left(z-l\text{sin}(\text{60})\right)}^2=l^2\end{array}\Rightarrow \{\begin{array}{c}x=\frac{l}{2}\\ y=l\sqrt{\frac{2}{3}}\\ z=\frac{l}{2\sqrt{3}}\end{array}\Rightarrow D=\left(\frac{l}{2},l\sqrt{\frac{2}{3}},\frac{l}{2\sqrt{3}}\right)$

Para hallar el centro del tetraedro a partir de sus vértices, primero he calculado el lugar geométrico de los puntos que están a igual distancia del vértice A y el vértice D, ya que las coordenadas x y z serán iguales que las del vértice D:

$\{\begin{array}{c}\sqrt{x^2+y^2+z^2}=\sqrt{{\left(x-\frac{l}{2}\right)}^2+{\left(y-\sqrt{\frac{2}{3}}\right)}^2+{\left(z-\frac{l}{2\sqrt{3}}\right)}^2}\\ x=\frac{l}{2}\\ z=\frac{l}{2\sqrt{3}}\end{array}\{O=\left(\frac{l}{2},\frac{l\sqrt{3}}{6\sqrt{2}},\frac{l}{2\sqrt{3}}\right)$

Y luego he resuelto el sistema formado por los tres planos para obtener el centro O. Para hallar el ángulo que forma el centro con los vértices, he trazado un triángulo isósceles entre el centro y dos vértices, y he hallado la distancia entre el vértice A y el centro O, que es el lado del dicho triángulo:

$\sqrt{{\left(\frac{l}{2}\right)}^2+{\left(\frac{l\sqrt{3}}{6\sqrt{2}}\right)}^2+{\left(\frac{l}{2\sqrt{3}}\right)}^2}=l\sqrt{\frac{1}{4}+\frac{3}{\text{72}}+\frac{1}{\text{12}}}=l\sqrt{\frac{3}{8}}$

Y, a partir del lado, he obtenido el ángulo β, que es el ángulo que forma el centro con los vértices (α es el ángulo agudo repetido en el triángulo isósceles):

$\{\begin{array}{c}\beta =\text{180}-\mathrm{2\alpha }\\ \text{cos}(\alpha )=\frac{l/2}{l\sqrt{\frac{3}{8}}}\end{array}\Rightarrow \{\begin{array}{c}\beta =\text{180}-\mathrm{2\alpha }\\ \alpha ={\text{cos}}^{-1}\left(\frac{1}{2\sqrt{\frac{3}{8}}}\right)\end{array}\Rightarrow \beta \approx \text{109}\text{.}\text{47}º$

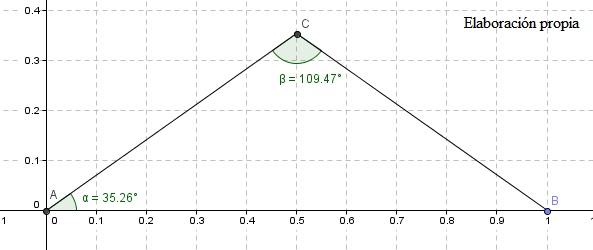
Que es muy parecido al ángulo que se da de forma natural en las moléculas de agua y de hielo I.

2.1.3. La geometría del hexágono

El hexágono es un polígono cerrado de seis lados, pero el que me interesa en esta monografía es el hexágono regular, que es el que se da en los copos de nieve. El hexágono regular tiene la particularidad de que todos sus lados y sus ángulos son iguales.

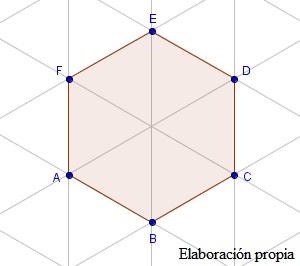
Perímetro:

El perímetro del hexágono si el lado es l será 6l.

Área:

El hexágono se puede descomponer como seis triángulos equiláteros para calcular su área (propiedad importante, en la que me basaré más adelante). Si el lado es l y a el apotema del hexágono (o la altura de cada uno de los triángulos) el área será

$6\frac{l\cdot a}{2}=\mathrm{3l}\cdot l\text{sin}(\text{60})=3\frac{l^2\sqrt{3}}{2}\approx l^{2}2\text{.}\text{5981}\text{.}\text{.}\text{.}$

Diagonales:

Las diagonales mayores (como por ejemplo entre A y D) son iguales al lado de un triángulo dos veces, luego es 2l.

Las diagonales menores (como por ejemplo entre A y C) son iguales al apotema dos veces, luego es $\mathrm{2a}=2\cdot l\text{sin}(\text{60})=l\sqrt{3}$

Ángulos:

Los ángulos interiores del hexágono son iguales a dos veces el ángulo de un triángulo rectángulo, así que será 120º.

Teselación:

El hexágono regular es una figura capaz de cubrir el plano indefinidamente si se sitúa otro hexágono igual a cada lado de un primer hexágono.

Simetría:

El hexágono tiene un grupo de simetría , lo que quiere decir que permanece invariante a cinco rotaciones parciales y, por supuesto, a una rotación completa. Por tanto, si giras un hexágono 60º, 120º, 180º, 240º, 300º o 360º la figura quedará igual que si no la hubieses rotado. También pasa lo mismo con las seis simetrías axiales, tres que pasan por las tres diagonales mayores y tres que pasan por los puntos medios de los lados opuestos entre si⁷.

2.2. Cálculo de áreas de copos de nieve

2.2.1. Los copos hexagonales

En este apartado veremos cómo se puede calcular el área de copos de nieve reales con el siguiente ejemplo:

Ahora, para calcular el valor de los distintos elementos del copo usaré las fórmulas del apartado anterior:

Si de extremo a extremo mide 1.4 eso quiere decir que el lado mide 0.7 mm (ya que la diagonal mayor mide 2l).

El perímetro es 6l=6·0.7=8.4 mm

El área es $3\frac{l^2\sqrt{3}}{2}=3\frac{0\text{.}{7}^2\sqrt{3}}{2}=0\text{.}\text{735}\sqrt{3}\approx 1\text{.}\text{27}$ mm².

Las diagonales mayores del copo miden 1.4 mm y las menores $l\sqrt{3}=0\text{.}7\sqrt{3}\approx 1\text{.}\text{21}$ mm.

Los copos hexagonales son los copos de mayor área en función del lado que puede haber, ya que el lado l es el lado del hexágono más pequeño que es capaz de abarcar al copo entero (consideración que emplearé de aquí en adelante).

2.2.2. Copos formados por capas

Pero hay pocos copos que sean totalmente hexagonales, la mayoría de ellos están formados heterogéneamente por ramificaciones y/o placas y su área es más difícil de calcular, por lo que hay que acudir a aproximaciones. Aún así nunca rompen con las formas hexagonales y los ángulos de 60º que les impone la estructura molecular del hielo. Aquí es cuando cobra protagonismo la anteriormente mencionada propiedad del hexágono para descomponerse en 6 triángulos equiláteros cuyo área (la mitad del producto base por altura) voy a usar como unidad básica para hacer los cálculos.

$\frac{l\cdot h}{2}=\frac{l\cdot l\text{sin}\text{60}}{2}=l^2\frac{\sqrt{3}/2}{2}=\frac{l^2\sqrt{3}}{4}$

Así incluso un copo formado por placas que no tenga forma hexagonal puede ser aproximado por triángulos equiláteros. Veamos el siguiente ejemplo:

En el caso de estos copos muchas veces es más fácil restar las partes que faltan que sumar las que están. El trozo que falta en este copo es muy similar a una forma descrita en el Anexo I llamada Curva de Von Kock. El área de este copo (A_h) es pues el área del hexágono menos 6 veces un triángulo de lado l/3 y doce de lado l/9:

$3\frac{l^2\sqrt{3}}{2}-6\frac{{\left(\frac{l}{3}\right)}^2\sqrt{3}}{4}-\text{12}\frac{{\left(\frac{l}{9}\right)}^2\sqrt{3}}{4}=l^2\frac{\text{35}\sqrt{3}}{\text{27}}\approx l^{2}2\text{.}\text{2453}$

2.2.3. Copos autosimilares y los fractales

Los copos de nieve no presentan un crecimiento dendrítico estable, sino que depende de las condiciones de temperatura y humedad reinantes en cada momento. Por eso la geometría de las ramificaciones que presentan los copos de nieve no puede ser descrita fácilmente. Acerca de eso Kenneth Libbrecht escribió en un artículo “As is typical for dendrites, the growth often exhibits some self-similar, fractal characteristics.”¹⁰.

La autosimilitud es una característica que aparece en la mayoría de los fractales y, como menciona en su artículo Kenneth Libbrecht, también aparece en los copos de nieve en ocasiones. La autosimilitud consiste en que tienen estructuras que se repiten a diferentes escalas. Por eso es útil en estos casos el uso de series para calcular los parámetros de una figura que presente esta característica porque para generarla se aplica recursivamente una transformación al conjunto, siendo el fractal la unión de todas las infinitas transformaciones (iteraciones) o simplemente el conjunto restante tras la última transformación. Aún así en los copos no se pueden dar transformaciones hasta el infinito, así que dejaré su área en función del número de iteraciones. De esta forma, en la notación que voy a usar, si tenemos un conjunto inicial I_o y le aplicamos una operación f(I) obtendremos f()I_o)=I₁.

Un ejemplo de un copo autosimilar es este:

El cálculo de esta área es bastante más complicado, y para modelizarlo he usado el software Geogebra:

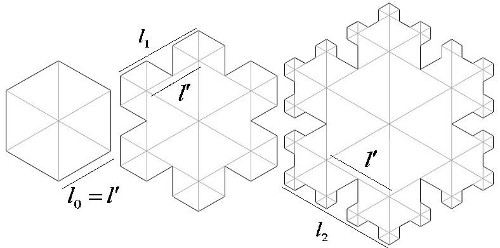
Como cada vez que la figura itera el lado del hexágono más pequeño que contiene al copo aumenta (l_n), lo primero que he hecho es calcularlo en función del lado del hexágono central, al que he llamado l' y de la iteración n:

$l_n=l^{\text{'}}+\frac{l^{\text{'}}}{2}+\frac{l^{\text{'}}}{2}\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)$

Para n≥1 Donde n es el número de iteraciones. Entonces el lado del hexágono central es:

$l_n=l^{\text{'}}\left(1+\frac{1}{2}+\frac{1}{2}\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)\right)=\frac{l^{\text{'}}}{2}\left(3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)\right)\Rightarrow l^{\text{'}}=\frac{{\mathrm{2l}}_n}{3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)}$

Y el área A_a del copo dependiendo del número n de iteraciones y el lado l es igual al número de triángulos de cada tamaño por el área de cada uno (nótese que el lado de cada triángulo depende de n):

$=6\frac{{\left(\frac{{\mathrm{2l}}_n}{3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)}\right)}^2\sqrt{3}}{4}+4\cdot 6\frac{{\left(\frac{{\mathrm{2l}}_n}{2\left(3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)\right)}\right)}^2\sqrt{3}}{4}+4\cdot 6\cdot 3\frac{{\left(\frac{{\mathrm{2l}}_n}{2\cdot 3\left(3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)\right)}\right)}^2\sqrt{3}}{4}\text{.}\text{.}\text{.}=$

$6\frac{l_{n^2}\sqrt{3}\left(2+\sum _{h=2}^n\frac{1}{3^{h-1}}\right)}{{\left(3+\left(\sum _{h=2}^n\frac{1}{3^{h-1}}\right)\right)}^2}$= $6\frac{l_{n^2}\sqrt{3}\left(2+\frac{1-{\left(1/3\right)}^n}{6\left(1-1/3\right)}\right)}{{\left(3+\left(\frac{1-{\left(1/3\right)}^n}{6\left(1-1/3\right)}\right)\right)}^2}=\frac{l_{n^2}\sqrt{3}\left(\text{12}+\frac{3-1/3^{n-1}}{4}\right)}{{\left(3+\left(\frac{1-{\left(1/3\right)}^n}{8}\right)\right)}^2}\approx l^{2}2\text{.}\text{2614}$

Para n→∞ y $l=\underset{n\to \infty }{\text{lim}}{l}_n$. Y así se puede calcular por series el área de los copos de nieve autosimilares.

2.2.4. Copos ramificados

Los copos ramificados son los más complicados de medir porque cualquier aproximación será relativamente inexacta, por eso es más fácil cuanto más ramas tenga. Veámoslo con un ejemplo:

En el caso de estos copos lo mejor es intentar aproximarlos a una forma general. En este caso concreto se parece mucho a una figura fractal conocida como el Copo de nieve de Von Kock. Los ángulos que forman todas las ramificaciones con la ramificación de la que salen son de 60º y, en conjunto, forman claramente un hexágono. Del mismo modo, en el copo de nieve de Von Kock los triángulos forman también 60º con respecto al triángulo del que salen y también forma en conjunto un hexágono.

El copo de nieve de Von kock es la figura que surge al juntar tres curvas de Von Kock (más información en el Anexo I) y es así:

Y como podemos ver en esta otra imagen es muy parecido:

El área de la figura (A_r) viene dada por la siguiente suma:

A_r=$\frac{l^{2}3\sqrt{3}}{4}+3\frac{{\left(\frac{l\sqrt{3}}{3}\right)}^2\sqrt{3}}{4}+3\cdot 4\frac{{\left(\frac{l\sqrt{3}}{3^2}\right)}^2\sqrt{3}}{4}+3\cdot 4^2\frac{{\left(\frac{l\sqrt{3}}{3^3}\right)}^2\sqrt{3}}{4}+\text{.}\text{.}\text{.}=\frac{l^{2}3\sqrt{3}}{4}\left(1+\sum _{n=1}^{\infty }\frac{4^{n-1}}{3^{\mathrm{2n}-1}}\right)$

En esta suma, el primer término es el área del triángulo inicial (I_o) más el área de los triángulos pequeños que van apareciendo al iterar la figura, multiplicado por el número de triángulos que aparecen.

A_r=$\frac{{\mathrm{3l}}^2\sqrt{3}}{4}\left(1+\frac{3}{4}\sum _{n=1}^n\frac{4^n}{3^{\mathrm{2n}}}\right)=\frac{{\mathrm{3l}}^2\sqrt{3}}{4}\left(1+\frac{1-{\left(4/9\right)}^n}{3\left(1-\frac{4}{3^2}\right)}\right)=\frac{{\mathrm{3l}}^2\sqrt{3}}{4}+\frac{{\mathrm{9l}}^2\sqrt{3}\left(1-{\left(4/9\right)}^n\right)}{\text{20}}=l^2\frac{6\sqrt{3}}{5}$

A_r=$l^2\frac{6\sqrt{3}}{5}\approx l^{2}2\text{.}\text{07846}\text{.}\text{.}\text{.}$

Para n→∞.

2.2.5. Copos mixtos

Los copos mixtos son copos que no están formados exclusivamente por ramificaciones ni por placas, sino por una mezcla de ambos. Eso hace que sean más irregulares a la hora de modelizarlos y que haga falta triángulos de distintos tamaños para calcular su área. Veamos un ejemplo:

Que puede ser aproximado de la siguiente manera:

En esta descomposición hay triángulos de tres tamaños distintos, de $l\frac{3}{\text{10}}$ (siendo l el lado del hexágono más pequeño que puede abarcar a la figura entera) los más grandes, de $l\frac{3}{\text{10}}$ los medianos y de l/10 los más pequeños. Así que si el área del copo (A_m) será:

A_m=$2\cdot 6\frac{{\left(l\frac{3}{\text{10}}\right)}^2\sqrt{3}}{4}+\left(7\cdot 6+6\right)\frac{{\left(l\frac{2}{\text{10}}\right)}^2\sqrt{3}}{4}+\text{10}\cdot 6\frac{{\left(\frac{l}{\text{10}}\right)}^2\sqrt{3}}{4}=l^2\frac{9\sqrt{3}}{\text{10}}\approx l^{2}1\text{.}\text{5588}\text{.}\text{.}\text{.}$

Y de igual forma se puede proceder con otros copos de esta clase.

2.2.6. Triángulos iguales

Igual que el hexágono se puede descomponer en triángulos equiláteros un triángulo equilátero también puede hacerlo:

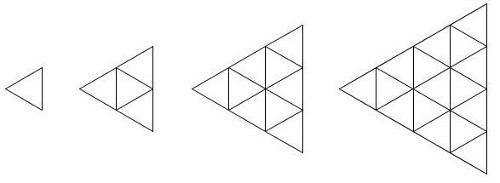
Así dependiendo del número d entre el cual que dividas el lado se obtienen un número C_d triángulos más pequeños:

C1	1
C2	1+3=4
C3	1+3+5=9
C4	1+3+5+7=16
Cd	d2

De esta forma el área de los copos de nieve anteriores puede calcularse más fácilmente (en algunos casos):

Para el copo formado por placas la fórmula anterior es esta:

A_h=$3\frac{l^2\sqrt{3}}{2}-6\frac{{\left(\frac{l}{3}\right)}^2\sqrt{3}}{4}-\text{12}\frac{{\left(\frac{l}{9}\right)}^2\sqrt{3}}{4}=l^2\frac{\text{35}\sqrt{3}}{\text{27}}\approx l^{2}2\text{.}\text{2453}$

Que quedaría así:

A_h=$\left(\text{81}\cdot 6-\text{11}\cdot 6\right)\frac{l^2\sqrt{3}}{\text{81}\cdot 4}=l^2\frac{\text{420}\sqrt{3}}{\text{324}}=l^2\frac{\text{35}\sqrt{3}}{\text{27}}\approx l^{2}2\text{.}\text{2453}$

Para el copo mixto la fórmula anterior es esta:

A_m=$2\cdot 6\frac{{\left(l\frac{3}{\text{10}}\right)}^2\sqrt{3}}{4}+\left(7\cdot 6+6\right)\frac{{\left(l\frac{2}{\text{10}}\right)}^2\sqrt{3}}{4}+\text{10}\cdot 6\frac{{\left(\frac{l}{\text{10}}\right)}^2\sqrt{3}}{4}=l^2\frac{9\sqrt{3}}{\text{10}}\approx l^{2}1\text{.}\text{5588}\text{.}\text{.}\text{.}$

Que quedaría así:

A_m=$\left(2\cdot 6\cdot 9+7\cdot 6\cdot 4+6\cdot 4+\text{10}\cdot 6\right)\frac{l^2\sqrt{3}}{\text{100}\cdot 4}=l^2\frac{\text{360}\sqrt{3}}{\text{400}}=l^2\frac{9\sqrt{3}}{\text{10}}\approx l^{2}1\text{.}\text{5588}\text{.}\text{.}\text{.}$

Sin embargo este método complica enormemente los cálculos de los otros dos copos:

Para el copo ramificado la fórmula anterior era esta:

A_r=$\frac{{\mathrm{3l}}^2\sqrt{3}}{4}\left(1+\frac{3}{4}\sum _{n=1}^n\frac{4^n}{3^{\mathrm{2n}}}\right)=\frac{{\mathrm{3l}}^2\sqrt{3}}{4}\left(1+\frac{1-{\left(4/9\right)}^n}{3\left(1-\frac{4}{3^2}\right)}\right)=\frac{{\mathrm{3l}}^2\sqrt{3}}{4}+\frac{{\mathrm{9l}}^2\sqrt{3}\left(1-{\left(4/9\right)}^n\right)}{\text{20}}=l^2\frac{6\sqrt{3}}{5}$

$l^2\frac{6\sqrt{3}}{5}\approx l^{2}2\text{.}\text{07846}\text{.}\text{.}\text{.}$

Para n→∞.

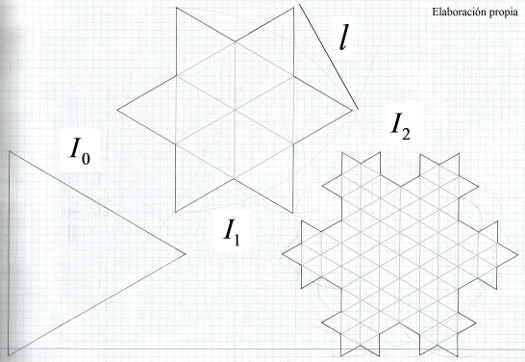
Una iteración I_n siempre puede ser dividida en triángulos de $l\sqrt{3}/3^n$ de lado (como se puede ver en la Figura 16), cuya área individual es de

$\begin{array}{c}\mathrm{}\\ \frac{l^{}3}{4}\Rightarrow \frac{{\left(\frac{l\sqrt{3}}{3^n}\right)}^2\sqrt{3}}{4}=\frac{l^2\sqrt{3}}{3^{\mathrm{2n}-1}4}\end{array}$

El número de triángulos que forman la iteración I_n viene dado por la sucesión $B_n={\mathrm{9A}}_{n-1}+4^{n-1}3$ siendo B_o=1, ya que cada triángulo existente en la iteración anterior se divide en nueve, y se añaden a la figura tres veces el número de lados pequeños de la iteración anterior. Por tanto, el área total de la figura será el número de triángulos de cada iteración multiplicado por el área de cada triángulo. He usado el programa informático Excel para hacer los cálculos de las series y del área de los triángulos hasta un número bastante alto de iteraciones (322). Los datos obtenidos aparecen recogidos en la siguiente tabla:

Iteración n	Número de triángulos $B_n={\mathrm{9A}}_{n-1}+4^{n-1}3$	Área de cada triángulo $\frac{\sqrt{3}}{3^{\mathrm{2n}-1}4}$	Área total
0	1	1,29903811	1,299038106
1	12	0,14433757	1,732050808
2	120	0,01603751	1,924500897
3	1128	0,00178195	2,010034271
4	10344	0,00019799	2,048049103
5	93864	2,1999·10-5	2,064944584
6	847848	2,4444·10-6	2,072453687
...	...	...	...
100	4,2498·1095	4,8907·10-96	2,078460969
...	...	...	...
322	2,953·10307	7,039·10-308	2,078460969

Como se ve en la tabla anterior el tiende a un límite cercano a l² 2.078460969, dado que los datos de la tabla son para l=1 y n variable. Intentando encontrar una expresión exacta para el área final, he buscado una función que contuviese los mismos puntos que la sucesión B_n he llegado a la siguiente función:

$B(x)=9^n+3\cdot 4^{n-1}+\sum _{x=1}^{n-1}{9}^x\left(3\cdot 4^{n-x-1}\right)=9^n+3\cdot 4^{n-1}+\frac{3^{\mathrm{2n}+1}}{5}-\frac{\text{27}\cdot 4^{n-1}}{5}$

Y por tanto la función del área será:

$f(n)=\frac{l^2\sqrt{3}}{3^{\mathrm{2n}-1}4}\left(9^n+3\cdot 4^{n-1}+\frac{3^{\mathrm{2n}+1}}{5}-\frac{\text{27}\cdot 4^{n-1}}{5}\right)$

Y el área final será:

A_r=$\underset{n\to \infty }{\text{lim}}\frac{l^2\sqrt{3}}{3^{\mathrm{2n}-1}4}\left(9^n+3\cdot 4^{n-1}+\frac{3^{\mathrm{2n}+1}}{5}-\frac{\text{27}\cdot 4^{n-1}}{5}\right)=l^2\frac{6\sqrt{3}}{5}\approx l^{2}2\text{.}\text{07842}\text{.}\text{.}\text{.}$

Para el copo autosimilar la fórmula anterior era esta:

A_a=$6\frac{l_{n^2}\sqrt{3}\left(2+\frac{1-{\left(1/3\right)}^n}{6\left(1-1/3\right)}\right)}{{\left(3+\left(\frac{1-{\left(1/3\right)}^n}{6\left(1-1/3\right)}\right)\right)}^2}=\frac{l_{n^2}\sqrt{3}\left(\text{12}+\frac{3-1/3^{n-1}}{4}\right)}{{\left(3+\left(\frac{1-{\left(1/3\right)}^n}{8}\right)\right)}^2}=l^2\frac{\sqrt{3}\left(\text{12}+3/4\right)}{{\left(3+1/8\right)}^2}\approx l^{2}2\text{.}\text{2614}\text{.}\text{.}\text{.}$

Cuando n→∞ y $l=\underset{n\to \infty }{\text{lim}}{l}_n$

Que, procediendo de forma análoga, sería de la siguiente forma:

A_a=$\underset{n\to \infty }{\text{lim}}\frac{{\left(\frac{\text{16}l}{\text{25}\cdot 3^2}\right)}^2\sqrt{3}}{4}\left(\text{12}\cdot 9^n+\text{24}\cdot 3^n+6\frac{9^n}{8}-4\cdot 3^n\right)=l^2\frac{\text{816}\sqrt{3}}{\text{625}}=l^{2}2\text{.}\text{2614}\text{.}\text{.}\text{.}$

Y, como se puede ver en estas dos últimas páginas, ninguno de los copos alcanza un área superior a $3\frac{l^2\sqrt{3}}{2}\approx l^{2}2\text{.}\text{59807621135331594}\text{.}\text{.}\text{.}$

Conclusiones

Los copos de nieve presentan una geometría hexagonal impuesta por la estructura molecular del hielo tipo I, que es el que se crea en las condiciones de presión y temperatura de la atmósfera, dado que el ángulo que forman los átomos de hidrogeno con el de oxígeno es muy parecido al del tetraedro, que a su vez constituye el elemento básico para formar redes hexagonales. El copo tiene por ello varias características iguales que el hexágono regular. Puede ser descompuesto en triángulos equiláteros y todos los ángulos que en el se forman son de 60º o de múltiplos del mismo. Esta geometría se da tanto en la escala más grande del copo (el copo entero) como en escalas más pequeñas (las ramificaciones). Por eso, algunos copos presentan autosimilitud, característica propia de los fractales.

Hay distintos tipos de copos de nieve según su forma: pueden ser hexagonales, formados por placas, autosimilares, ramificados o mixtos. El área de un copo de nieve es igual o inferior a veces su lado donde l es el lado del hexágono de menor tamaño que contiene al copo. El área de un copo de nieve se puede calcular aproximándola por construcciones hechas sólo de triángulos equiláteros de dos formas distintas: sumando triángulos equiláteros de distintos tamaños (útil para los copos autosimilares), o reduciendo todos los triángulos al tamaño del más pequeño de ellos usando múltiplos (útil con los mixtos y los formados por placas).

Bibliografía

Libros consultados:

• Caballero Hurtado, Alfonso Víctor: Abre los ojos al Ensamblador. Capítulo 32. Libro on-line. Consultado el 31/12/12 http://www.abreojosensamblador.net/Productos/AOE/html/Pags/Cap32.html#Def
• Guerrero, Manuel: El agua libro on-line. Ed.: Fondo de Cultura Económica. México 1991 Consultado el 10/12/12 http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen2/ciencia3/102/html/sec_4.html
• Lide, David R.: CRC Handbook of Chemistry and Physics. Ed.: National Institute of Standards and Technology 2010
• Mandelbrot, Benoit B.: The fractal geometry of nature. Ed.: Macmillan 1982
• Navarro, Joaquín: Al otro lado del espejo. La simetría en matemáticas. Ed.: RBA Navarra 2012.

Artículos consultados:

• Libbrecht, Kenneth G.: "The physics of snow crystals", artículo publicado en Reports on Progress in Physics. Vol.:68 Número 4, Abril de 2005.
• Schauerhammer, Ralf: "El copo de nieve de seis ángulos y la geometría pentagonal". Artículo publicado en la revista alemana Fusión en la edición de invierno de 2002.

Webs consultadas:

• http://bifi.es/~jsancho/estructuramacromoleculas/1aguaylasmembranasbiologicas/hielo.jpg Consultada el 10/12/12
• http://www.cg.tuwien.ac.at/courses/Fraktale/PDF/fractals3.pdf Consultado el día 1/1/13
• http://www.its.caltech.edu/~atomic/snowcrystals/ Consultada el día 23/1/2013
• http://www.its.caltech.edu/~atomic/snowcrystals/photos/w041219b055.jpg Consultada el día 24/02/13
• http://www.its.caltech.edu/~atomic/snowcrystals/photos2/w050207a069.jpg Consultado el día 24/02/13
• http://www.its.caltech.edu/~atomic/snowcrystals/photos3/w050207b038.jpg Consultada el 24/02/13
• http://www.nature.com/news/2004/041231/full/news041229-8.html Consultado el día 5/1/2013
• http://www.scientificamerican.com/slideshow.cfm?id=no-two-alike-snowflake-photography#9 Consultada el día 25/1/2013

Anexo: Fractales y la curva de Von Kock

Fractal se define como un conjunto cuya dimensión topológica es menor que su dimensión de Hausdorff-Besicovich (inecuación de Szpilrajn). Pero la definición es un poco inexacta dado que hay fractales cuyas dimensiones son iguales. La dimensión topológica es aquella a la que estamos acostumbrados: el número de direcciones perpendiculares entre sí que existe en el conjunto. La dimensión de Hausdorff-Besicovicht, sin embargo, no es una dimensión topológica, sino métrica¹⁴.

Llamemos D_T a la dimensión topológica y D a la dimensión de Hausdorff-Besicovich. Para los objetos no fractales se cumple que D_T=D. Si N(L) es el número de segmentos iguales de longitud L en los que partimos un segmento de longitud l se cumple que:

l=N(L)·L^D

Para el caso de un segmento (D_T=1) de longitud l=1 que dividiésemos en partes de longitud L=1/2, se cumple que:

1=2(1/2)^D⇒D=1

Y en general es fácil ver que, con independencia del número de trozos en que se divida el segmento, se cumple:

l=n(l/n)^D⇒D=1

Para el caso de un cuadrado (D_T=2) lado 1 que dividiésemos en N(L)=4 cuadrados de lado L=1/2, se cumple que:

1=4(1/2)^D⇒D=2

Para el caso de un cuadrado de lado 3 que dividiésemos en N(L)=16 cuadrados de lado L=3/4 obtenemos el mismo resultado:

9=16(3/4)^D⇒D=2

Y en general es fácil comprobar que para cualquier cuadrado se cumple:

l²=n²(l/n)^D⇒D=2

Luego desde la ecuación general podemos obtener una expresión para D si la longitud l=1, y por tanto¹⁵ logl=0 (en la ecuación no influye la base del logaritmo):

$l=N(L)\cdot L^D\Rightarrow \text{log}l=\text{log}N(L)+D\text{log}(L)\Rightarrow D=-\frac{\text{log}N(L)}{\text{log}L}\Rightarrow D=\frac{\text{log}N(L)}{\text{log}\frac{1}{L}}$

Uno de los fractales más conocidos es la curva de Von Kock:

Helge Von Kock describió esta curva cuando buscaba una curva continua que no fuese derivable en ninguno de sus puntos. Para conseguir esto, Kock se basó en que los puntos de ruptura de una curva quebrada no son derivables (no tienen una tangente única), ya que sus derivadas por la derecha y por la izquierda no son iguales. La curva de Von Kock parte de un segmento de longitud l como figura inicial (I_o) y se le aplica recursivamente una transformación consistente en dividir en tercios el segmento y poner, en lugar del tercio central, dos tercios formando un ángulo de 60º con el segmento original, formándose así un triángulo equilátero entre el tercio que desaparece y los dos que aparecen en su lugar.

Al ser una línea, la dimensión topológica que le corresponde es D_T=1 y, dado que la figura es un segmento que se divide en N(L)=4 segmentos de longitud L=1/3 (suponiendo que l=1), la dimensión de Hausdorff-Besicovich será:

$D=\frac{\text{log}N(L)}{\text{log}\frac{1}{L}}=\frac{\text{log}4}{\text{log}\frac{1}{1/3}}=\frac{\text{log}4}{\text{log}3}\approx 1\text{.}\text{2686}$

Así que cumple la inecuación de Szpilrajn D_T≤D⇒1≤1.2686

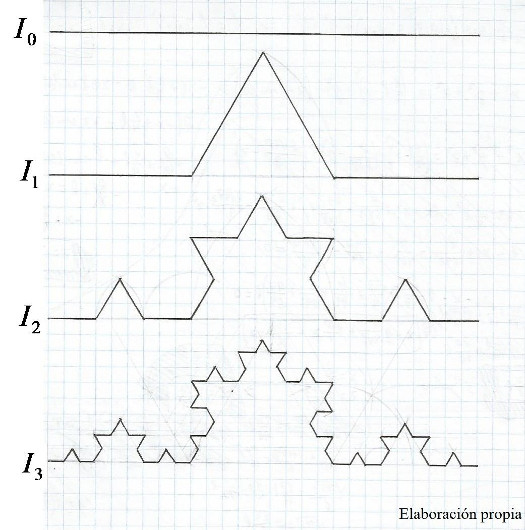
Los puntos no derivables siguen la siguiente sucesión 0, 3, 15, 63… que llamaré P_n y cuya expresión es P_n=4P_n-1+3, siendo P_o=O, ya que el primer tercio de la iteración I_n es igual a la iteración I_n-1 sólo que tres veces más pequeña, por lo que en I_n hay cuatro curvas como la de I_n-1 , y, por tanto, 4 veces más puntos que en la iteración anterior, más tres puntos de ruptura que forman las cuatro curvas. Y $\underset{n\to \infty }{\text{lim}}{P}_n=\infty$ por lo que la curva de Von Kock no es derivable en ningún punto, ya que todos los puntos de I_∞ son de ruptura.